Bruggen
De bruggen geven in HEC-RAS aanvankelijk een flink groter verval dan in SOBEK: alleen al over de eerste brug 38 cm om 14 cm. Dit verschil moet verklaard en opgelost worden.
In SOBEK worden bruggen doorgaans geschematiseerd in de vorm van objecten van het type ‘Flow - Bridge’. Waterschap Limburg is echter van dit knooptype afgestapt omdat SOBEK de afvoerfactor \(\mu\) kunstmatig begrenst op 1.0. Volgens het waterschap resulteerde deze begrenzing in veel simulaties in een onrealistisch groot verval over de kunstwerken.
Daarom heeft Waterschap Limburg enkele jaren terug besloten bruggen alleen nog maar te schematiseren met knopen van het type ‘extra resistance node’. Op knopen van dit type wordt als functie van de waterhoogte een weerstandswaarde \(\xi\) (KSI) toegekend (s2/m5). Ook \(\xi\) maakt gebruik van afvoerfactor \(\mu\), maar doordat we die nu zelf berekenen wordt hij niet afgekapt.
Om de parameterwaarden te kunnen berekenen ontwikkelde Hydroconsult indertijd een algoritme.
Intern in SOBEK wordt de waarde van \(\xi\) vermenigvuldigd met het kwadraat van het debiet. De uitkomst geeft het extra verval in m:
\[\Delta H = \xi \times Q \times |Q|\]
Om de implementatie van de bruggen goed te kunnen vergelijken tussen Definitief Ontwerp, SOBEK en HEC-RAS nemen we het addendum van Hydrocosult’s rapport: (Bosch 2021) als vertrekpunt voor onze analyse:
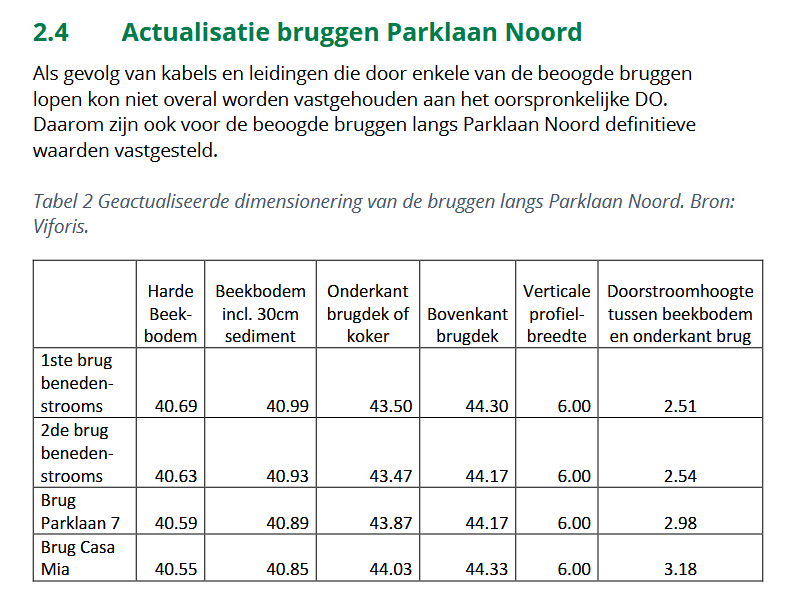
In dit addendum staat dat enkele bruggen moesten worden verlaagd ivm kabels en leidingen, en dat hier dus is afgeweken van het oorspronkelijk DO. We nemen de eerste brug benedenstrooms van Engelenkamp als casus voor een onderlinge vergelijking tussen SOBEK en HEC-RAS.
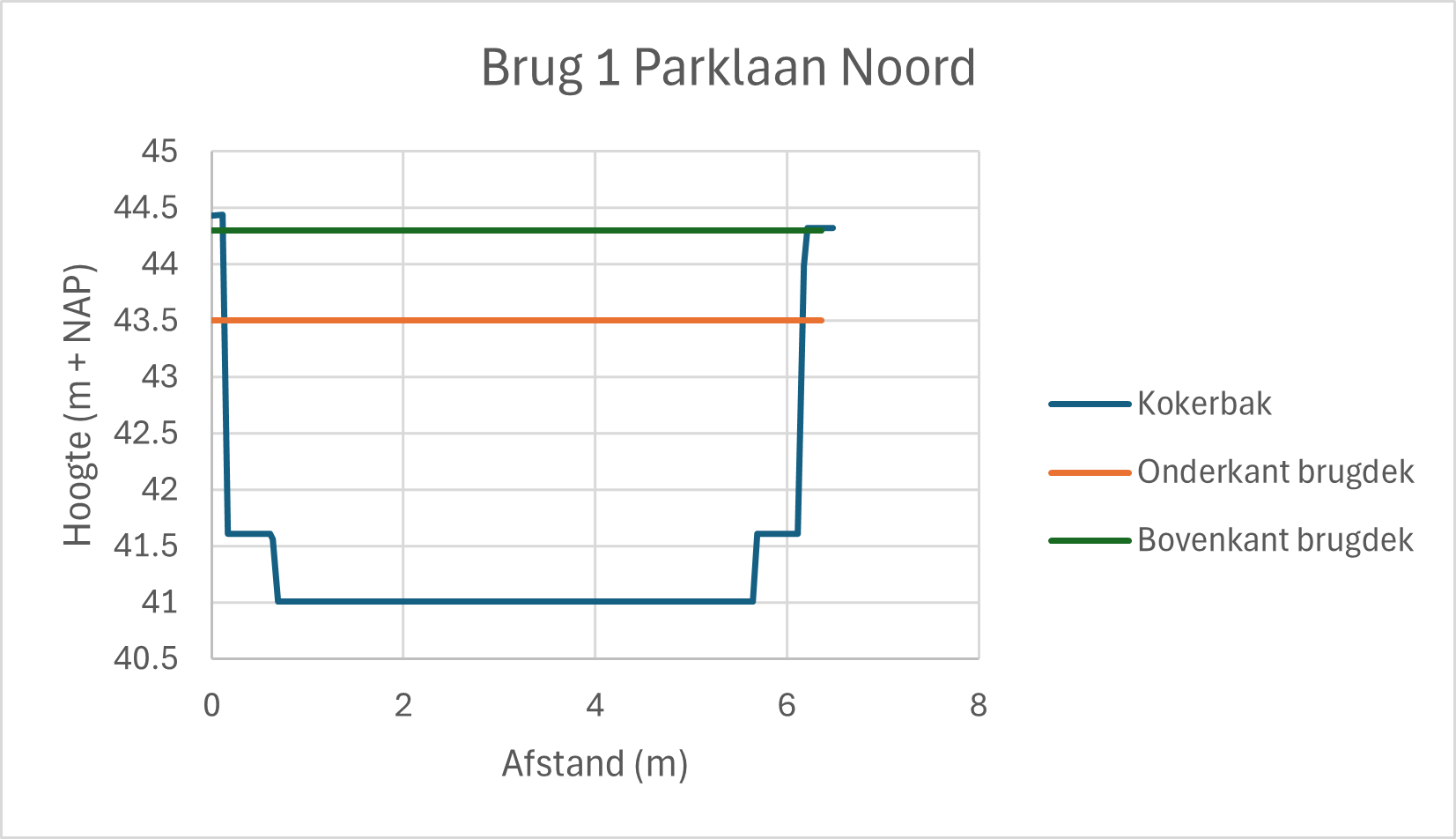
Conform deze tabel en het ontwerp van de kokerbak zou de brug er als volgt uitzien:
Onderkant brugdek ligt op 43.50 m NAP en bovenkant brugdek op 44.30 m NAP.
Echter in het DO-model van SOBEK werd deze brug geïmplementeerd met o.a. de volgende weerstandswaarden voor \(\xi\):
| Waterhoogte (m NAP) | \(\xi\) |
|---|---|
| 44.29 | 0 |
| 44.3 | 2.345245E-05 |
| 44.6 | 2.432356E-05 |
| 44.61 | 2.435749E-05 |
| 45.1 | 2.723007E-05 |
Aan de waarden in de tabel is te zien dat de extra weerstand in het model van deze brug pas begint bij 44.30 m + NAP. Volgens het gecorrigeerde DO was dit echter de bóvenkant brugdek, en niet de onderkant. Dit suggereert dat de verlaging als gevolg van de kabels en leidingen niet is doorgevoerd in deze modelvariant van het DO.
We moeten de weerstandswaarden dus actualiseren.
Actualiseren weerstandswaarden
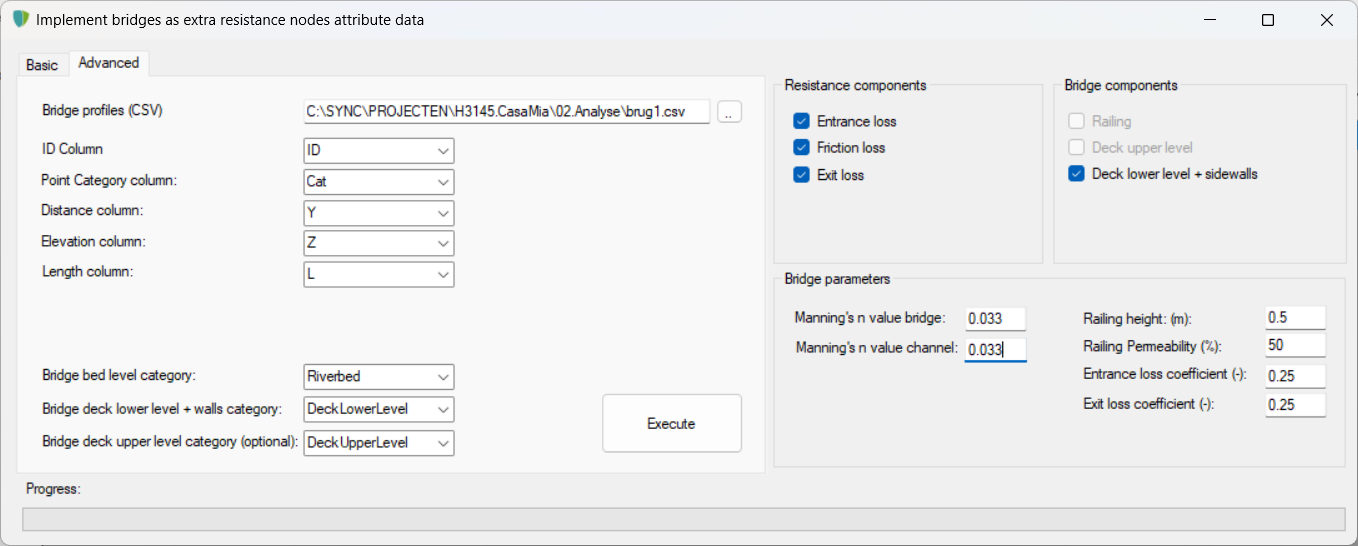
We herberekenen nu de weerstandswaarden op basis van de brugdekhoogtes uit de tabel. Dit doen we met een functionaliteit uit HydroToolbox (Hydroconsult).
We importeren het dwarsprofiel van de beek en een profiel van onderkant brugdek en bovenkant brugdek via een .CSV-bestand en stellen de ruwheidswaarden en energieverliescoëfficiënten in. Met het resultaat kunnen we het theoretisch verval over het kunstwerk uitrekenen. Dit doen we door de waarde voor \(\xi\) te vermenigvuldigen met het kwadraat van de afvoer (45 m3/s).
Het resultaat lijkt nog altijd niet op dat van HEC-RAS. Het verval over bijvoorbeeld de eerste brug is wel iets toegenomen (van 14 naar 17,6 cm), maar dit ligt nog altijd ver verwijderd van de 38 cm die we in HEC-RAS zagen.
Verificatie methode ‘extra resistance node’
Om de oorzaak van het verschil te achterhalen onderzoeken we eerst of de methode zoals door ons geïmplementeerd wiskundig en natuurkundig correct is. Het reviewen van code is iets waar LLM’s (Large Language Models) bij uitstek geschikt voor zijn. Vandaar dat we, onafhankelijk van elkaar zowel ChatGPT (OpenAI 2024) als Claude (Anthropic 2024) de broncode lieten reviewen.
Dit was de prompt:
Please review this code. It is designed to compute extra resistance in hydraulic channels as caused by bridges. In particular I need you to check whether the equations are correct and whether they are being processed correctly. Do not take my comments for granted but check thoroughly. Pay special attention to how the various energy loss components are combined and implemented in the overall equation.
ChatGPT 4o geeft het volgende oordeel:
- Your equations are implemented correctly.
- The friction, entrance, and exit losses are correctly combined
- The final KSI equation is implemented correctly
- The function CalculateFrictionLossChezy() correctly computes friction loss
- Correct formula for Manning’s n
Het model geeft daarnaast nog enkele aanbevelingen aangaande de randen van het toepassingsbereik.
Claude Sonnet 3.5 geeft het volgende oordeel:
The overall implementation appears mathematically sound and follows standard hydraulic engineering principles for bridge head loss calculations. The combination of energy losses and their translation into the KSI coefficient is handled correctly.
Eventuele fouten in de berekening van de extra weerstandswaarden kunnen we dus afstrepen als mogelijke oorzaak voor het verschil tussen SOBEK en HEC-RAS.
Vergelijking verliescoëfficiënten HEC-RAS en SOBEK
Een andere mogelijke oorzaak voor de verschillen tussen SOBEK en HEC-RAS zit hem in eventuele verschillen in toegepaste intree- en uittreeverliescoëfficiënten.
Alvorens deze verschillen te analyseren bekijken we eerst hoe SOBEK en HEC-RAS de afvoer door bruggen berekenen. Beide modellen passen in de basis de klassieke brugformule toe. Althans indien bij HEC-RAS gekozen wordt voor de optie ‘Pressure and or Weir flow’ en in SOBEK voor ‘Flow - Bridges’.
HEC-RAS: \[ Q = C_d A \sqrt{2g \Delta H} \]
In inverse vorm:
\[ \Delta H = \frac{1}{2g} \left( \frac{Q}{C_d A} \right)^2 \]
SOBEK:
\[ Q = \mu A \sqrt{2g \Delta H} \]
Waarbij afvoerfactor \(\mu\) wordt bepaald door:
\[ \mu = \frac{1}{\sqrt{\xi_i + \xi_f + \xi_o}} \]
\(\mu\) is een composiet van weerstanden als gevolg van intree, uittree en wrijving.
Een groot verschil tussen SOBEK en HEC-RAS is echter dat de gebruiker in HEC-RAS de waarde voor Cd expliciet opgeeft, en dat SOBEK de waarde voor \(\mu\) zelf berekent op basis van de dimensies van de brug en het beekprofiel.
Echter omdat wij zoals gezegd werken met objecten van het type ‘Extra resistance node’ moeten we de waarde voor \(\mu\) zelf berekenen.
Vergelijking Extra Resistance Node: \[ \Delta H = \xi \times Q \times |Q| \]
waarin: \[\xi = \frac{1}{\mu^2 A^2 2g}\]
We konden de waarden voor \(\xi\) vrij eenvoudig converteren naar de equivalente afvoerfactor Cd voor HEC-RAS. Hierbij bleek dat de waarde voor Cd structureel groter dan 1 wordt: Cd zou een waarde van tussen de 1.4 en 1.7 krijgen.
Voorlopige conclusie
De aanvankelijk grote verschillen tussen SOBEK en D-Hydro hebben twee oorzaken:
- Enkele verlagingen van de bruggen ten opzichte van het DO (gepubliceerd in een addendum) waren niet doorgevoerd in de modelschematisatie die we hier als referentie hadden genomen. Het effect hiervan op de waterhoogtes ligt in de orde grootte van enkele centimeters